- Watch Tom Dwan explain short-deck poker, aka 6-Plus Hold’em, the game played by some of the biggest cash game players in the world.
- Check out the short deck hand rankings. Martingale Europe Limited operates according to Maltese Law, and is regulated by the Malta Gaming Authority (MGA) under license MGA/CRP/688/2019 issued on 1/10/2020 in the name of the reporting entity bwin Holdings (Malta) Limited, located at Penthouse Spinola Business Centre, Number 46, St Christopher Street, Valletta, Malta, VLT 1464.
- Equity calculator for short deck and full deck hold'em poker games with hand history storage.
Six-plus hold 'em (also known as short-deck hold 'em) is a community card poker game variant of Texas hold 'em, where the 2 through 5 cards are removed from the deck. Each player is dealt two cards face down and seeks to make the best five card poker hand from any combination of the seven cards (five community cards and their own two hole cards).

Note: These rules are general enough to apply to your Short Deck Poker games regardless of which hand rankings are used. Tip #1: Play more suited hands and pocket pairs (and play them more aggressively) This is basically the opposite of tip #1. Since flushes and trips increase in value, suited hands and pocket pairs increase in value. Poker Starting Hand Chart (6-max Cash, 100bb): Hand Chart Notation Getting to know which hands to play and in which positions is even more important than the actual hand. This 6-max Cash Hand Chart details the hands you should play and the position. 5-minute poker hand analysis wrap-up. Hand analysis is the bread and butter of your off-table work, and repeating this quick method will undoubtedly make you a much stronger player. If you are serious about getting better at poker, I think you should analyze at least one hand every day to keep your skills sharp and your trajectory upward. Nice hand: nhs: Nice hands (usually used when a great hand beats a good hand) NL: No limit: o: Off-suit, written as 78o: ott: Over the top: PL: Pot limit: pls: Please: Q: Queen: qed: Math geekspeak for so it is proven: rgp: Rec.gambling.poker (a Usenet group) rofl: Rolling on the floor laughing: ru: Are you: s: Spades: sb: Small blind: sob: I.
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |

___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
___________________________________________________________________________
2017 – Dan Ma
Introduction
Shorthanded poker is played with six or less players at the table, making it necessary to give more action than you would in full-ring poker and forcing you to play more hands in order to win.
It is a fun and exciting way to play and many of the top online winners excel at short-handed play. They prefer these types of games because they are less mechanical and, as such, involve an increase in psychological play and mind games with one's opponents.
As well, they are able to win money from less skilled players more often than in full-ring games. This is mostly due to the fact that you play more hands and are therefore in a position to make more decisions when playing. And, remember, it is by making the correct decisions that a poker player makes their money.
In addition, the added psychological factors mean that you must adapt your play to the ebb and flow of the game, thus making it harder to provide general advice that will be true for most situations. And, while advising play is difficult in all forms of poker, it is especially so in short-handed play.
Basic Shorthanded Limit Poker Strategy
The key skill to possess for successful shorthanded play is aggressiveness. In shorthanded play, the price per hand is higher, you have to play more hands, and you have to play them more aggressively.
You need to be raising and re-raising with many playable hands in order to isolate a lone opponent and take the lead. In Limit Hold'em, and particularly in shorthanded Limit Hold'em, you must push very small edges and think about the money you will make in the long run by doing this.
You cannot allow a bad streak to affect you and make you scared of pushing. Basically, most hands worth playing are now worth raising with. This is a key concept in shorthanded Limit Hold'em, and is especially true when you are in late position.
Hand Selection
In shorthanded Hold'em, the starting hands have a different value than they do in full-ring games. The small pairs, hands such as A-x, and big connectors like KJ and QT, increase in value, and small suited connectors such as 76s and 87s, decrease in value.
This is because in any given hand you have to worry less, for example, about someone holding a bigger ace when you hold an A-x, or a bigger king when you hold something like K-T. The problem with small suited connectors, however, is that if you do not improve you cannot win with them in a showdown, whereas with A-x or even K-x, that will frequently occur.
As well, you will find yourself in fewer situations that involve top-pair and kicker trouble than you likely would in a full-ring game. And, your opponents will give action with hands like J-x on a flop of Q-J-3, so most of the time you can bet a Q-2 on this flop for value all the way to the river, whereas, in a full-ring game you would be very wary about playing this hand strong.
With the small suited connectors, the pot will seldom give you the correct odds to play them pre-flop. So, for instance, say you are on the button in a five-handed game, even if both players acting before you limp-in, it might still be correct to throw them away. Instead, an occasional raise is probably a better play in order to vary your game.
The Blinds
Shorthand Poker Hands Signals
When you are in the blinds and the pot has been raised, you can worry a lot less about being dominated, and should instead focus on defending with many hands that you would have folded had the game been ten-handed.
For example, in a full-ring game, holding an A-8 off-suit in the big blind when the under-the-gun player raises would result in an automatic fold against all but the worst players. However, in short-handed play, this is a hand that you would frequently re-raise with and seldom fold.
Early Position
You ought to mix-up your play by varying limping and raising with an assortment of hands. You should remain selective and not play hands like A-2 off-suit, K-9 suited, or worse. Essentially, you want a suited A-x, an A-9 off-suit or higher, a KQ off-suit, a QJ off-suit, any big suited connector like JTs, or pairs from sixes and up, and you want to frequently raise with them.
Shorthand Poker Hands Meaning
Late Position
In late position, most hands become raising or re-raising hands. Even hands such as JTs can be a re-raising hand because of the extra value you will gain from taking the lead and having position. Generally, you can re-raise with basically any pair, A-x suited, or any big suited connector.
Shorthand Poker Hands Emoji
Short Deck Top Hands
Post-Flop
On the flop you must continue to play aggressively, especially if you were the aggressor pre-flop and it is a heads-up pot. Short-handed poker is mostly about winning pots by being aggressive with bluffs and semi-bluffs, in particular.
Short Deck Hands
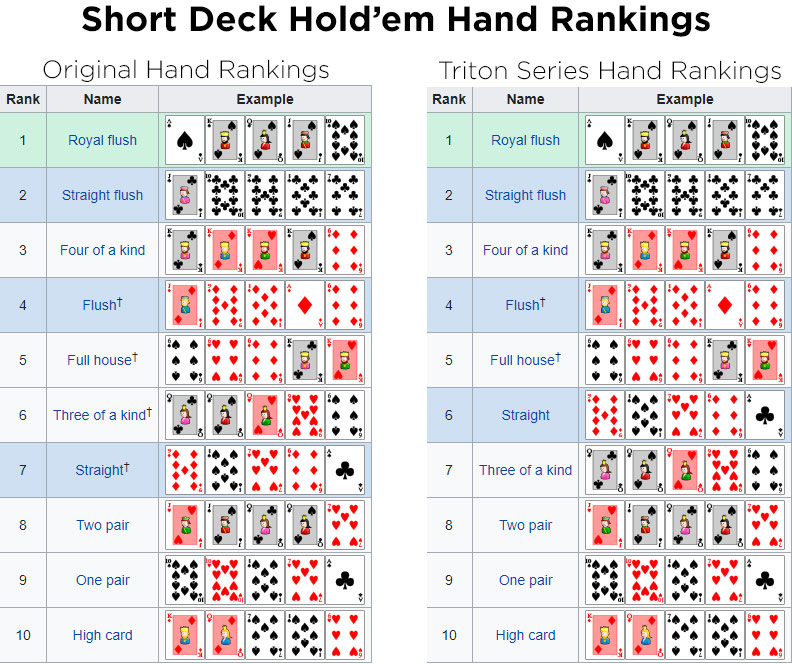
Short Deck Poker Hands
Most players will play any kind of flush or straight draw as though it was the nuts on the flop, and it is correct to do so in most cases. It takes experience and skill to know when to bet an unimproved AK for value on the river and when to fold top pair, and this is what you should set out to master.